파이토치 ANN
기록 - 2022/01/29
<오염된 이미지 문제 >
-> 이미지 처리를 위해 만들어 두었던 weired_function()함수에 버그가 들어가 오염된 이미지가 만들어짐, 원본 이미지를 복원하기 위함
1. weired_function() 함수의 소스코드 분석
2. 분석을 토대로 weired_function() 함수의 동작을 반대로 이행하는 함수를 구현한다
3. 2에서 구현한 함수에 오염된 이미지를 입력해서 복구된 이미지를 출력한다.
사고과정
1. 오염된 이미지(broken_image)와 크기가 같은 랜덤텐서(random_tensor)를 생성한다. (랜덤텐서는 오염된 이미지와 크기가 같은 무작위 이미지 텐서를 의미합니다)
2. 랜덤 텐서를 weired_function() 함수에 입력해 똑같이 오염된 이미지를 가설이라고 부른다.
(1) [사실] 원본 이미지가 weired_function()함수에 입력되어 오염된 이미지를 출력했다.
(2)[사실] 인위적으로 생성한 무작위 이미지가 weired_function() 함수에 입력되어 가설을 출력했다
3. 가설과 오염된 이미지가 같다면, 무작위 이미지와 원본 이미지도 같을 것이다.
4. 그러므로 weired_function(random_tensor) = broken_image 관계가 성립하도록 만든다
-> 머신러닝 모델이 학습한다는 것은 모델이 출력한 결괏값과 정답의 차이, 즉 오차가 최소화된다는 뜻이다. 이 문제에서 오차는 위에 언급한 '가설'과 원본 이미지가 wired_function() 함수를 통해 오염되기 전의 이미지(정답) 사이의 거리입니다. 이 오찻값이 최솟값이 되오록 랜덤텐서(random_tensor)를 바꿔주는 것이 최종적인 목표입니다
-> 파이토치 Autograd 패키지를 이용하면 오차를 출력하는 함수의 기울기(미분값)에 해당하는것을 찾을 수 있다. 미분을 통해 구한 기울기의 반대방향으로 가면 오찻값이 줄어들고 이것을 반복하다면 오찻값이 최소가 되는데. 오찻값이 최소가 되었을때 랜덤텐서는 오염되기 전의 이미지와 같아질것입니다. 이렇게 랜덤 텐서를 미분값의 반대 방향으로 조금씩 이동하면서 모델을 최적화 하는것이 경사하강법 알고리즘 입니다.
import torch
import pickle
import matplotlib.pyplot as plt
#오염된 이미지 bk 를 파이토치의 텐서 형태로 읽은후 어떻게 보이는지 확인해 보기
bk = torch.FloatTensor(pickle.load(open('./broken_image_t.p', 'rb'), encoding='latin1'))
plt.imshow(bk.view(100,100))
<matplotlib.image.AxesImage at 0x7fe89b4791f0>
#이미지를 오염시키는 weired_function()코드 (이 코드에 대한 이해는 중요하지 않음 )
def weired_fc(x, n_iter=5):
h = x
filt = torch.tensor([-1./3, 1./3, -1./3])
for i in range(n_iter):
zero_tensor = torch.tensor([1.0*0])
h_l = torch.cat((zero_tensor, h[:-1]), 0)
h_r = torch.cat((h[1:], zero_tensor), 0)
h = filt[0] * h + filt[2] * h_l + filt[1] * h_r
if i % 2 == 0:
h = torch.cat( (h[h.shape[0]//2:], h[:h.shape[0]//2]), 0)
return h
#무작위 텐서(random_tensor)를 weired_fc()함수에 입력해 얻은 가설텐서와 오염된 이미지 사이의 오차를 구하는 함수를 구현
#torch.dist() 는 두 텐서 사이의 거리를 구하는 함수 (가설과 깨진 이미지 사이의 거리를 오차값으로 설정 )
def distance_loss(hypothesis, bk):
return torch.dist(hypothesis, bk)
#무작위 텐서 생성
random_tensor = torch.randn(10000, dtype = torch.float)
#러닝레이트 설정
lr = 0.8
#오차함수를 random_tensor로 미분을 해야하기 때문에 requires_grad를 True로 설정
for i in range(0, 20000):
random_tensor.requires_grad_(True)
hypothesis = weired_fc(random_tensor)
loss = distance_loss(hypothesis, bk) #가설과 깨진이미지 사이의 거리값을 오차값으로 지정하고
loss.backward() #backward 함수를 호출해 loss를 random_tensor로 미분
with torch.no_grad():
random_tensor = random_tensor - lr*random_tensor.grad #random_tensor.grad에는 loss의 기울기, 즉 loss가 최댓점이 되는
#곳들의 방향이 들어있고 이방향의 반대쪽으로 random_tensor를 학습률 lr 만큼 이동시킨다.
if i % 1000 == 0 :
print('Loss at {} = {}'.format(i, loss.item()))
plt.imshow(random_tensor.view(100, 100).data)
Loss at 0 = 0.021167831495404243
Loss at 1000 = 0.021168140694499016
Loss at 2000 = 0.021167609840631485
Loss at 3000 = 0.021167607977986336
Loss at 4000 = 0.02117043361067772
Loss at 5000 = 0.021169718354940414
Loss at 6000 = 0.02117188833653927
Loss at 7000 = 0.021172119304537773
Loss at 8000 = 0.021172795444726944
Loss at 9000 = 0.021172959357500076
Loss at 10000 = 0.021173644810914993
Loss at 11000 = 0.021174732595682144
Loss at 12000 = 0.021174436435103416
Loss at 13000 = 0.0211744774132967
Loss at 14000 = 0.021174918860197067
Loss at 15000 = 0.021174293011426926
Loss at 16000 = 0.02117433026432991
Loss at 17000 = 0.021173788234591484
Loss at 18000 = 0.021174758672714233
Loss at 19000 = 0.02117428183555603
<matplotlib.image.AxesImage at 0x7fe89b534790>
신경망 모델 구현하기(인공신경망 ANN)
분류 모델 구현하기
#make_blobs : 예제용 데이터셋을 만들어 주는 함수로 데이터를 2차원 벡터 형태로 만들어준다(인덱스 레이블 형태)
n_dim = 2
x_train, y_train = make_blobs(n_samples=80, n_features=n_dim, centers=[[1,1],[-1,-1],[1,-1],[-1,1]],
shuffle=True, cluster_std = 0.3)
x_test, y_test = make_blobs(n_samples=20, n_features=n_dim, centers=[[1,1],[-1,-1],[1,-1],[-1,1]],
shuffle=True, cluster_std = 0.3)
print(y_train)
[3 2 0 0 1 2 3 1 2 0 1 2 2 0 1 2 1 3 1 2 3 0 0 1 3 0 2 1 1 0 2 1 1 2 3 3 2
3 3 0 3 1 0 3 0 0 1 3 0 2 1 3 3 2 3 1 0 2 1 3 2 2 2 3 1 1 0 0 3 0 0 2 2 3
3 1 0 2 0 1]
def label_map(y_, from_, to_):
y = numpy.copy(y_)
for f in from_:
y[y_ == f] = to_
return y
print(y_train)
y_train = label_map(y_train, [0,1],0)
y_train = label_map(y_train, [2,3],1)
y_test = label_map(y_test, [0,1],0)
y_test = label_map(y_test, [2,3],1)
print(y_train)
[3 2 0 0 1 2 3 1 2 0 1 2 2 0 1 2 1 3 1 2 3 0 0 1 3 0 2 1 1 0 2 1 1 2 3 3 2
3 3 0 3 1 0 3 0 0 1 3 0 2 1 3 3 2 3 1 0 2 1 3 2 2 2 3 1 1 0 0 3 0 0 2 2 3
3 1 0 2 0 1]
[1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 1 1
1 1 0 1 0 0 1 0 0 0 1 0 1 0 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 0 0 1 0 0 1 1 1
1 0 0 1 0 0]
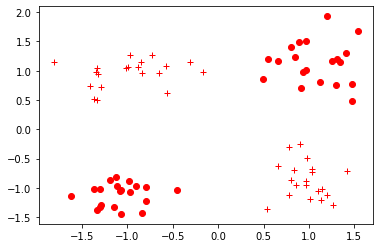
def vis_data(x,y = None, c = 'r'):
if y is None:
y = [None] * len(x)
for x_, y_ in zip(x,y):
if y_ is None:
plt.plot(x_[0], x_[1], '*', markerfacecolor = 'none', markeredgecolor=c)
else :
plt.plot(x_[0], x_[1], c+'o' if y_ == 0 else c+'+')
plt.figure()
vis_data(x_train, y_train, c='r')
plt.show()
#넘파이 벡터 -> 파이토치 텐서로 변경
x_train = torch.FloatTensor(x_train)
x_test = torch.FloatTensor(x_test)
y_train = torch.FloatTensor(y_train)
y_test = torch.FloatTensor(y_test)
#신경망 모델 구현 torch.nn.Module
class NeuralNet(torch.nn.Module):
def __init__(self, input_size, hidden_size):
super(NeuralNet, self).__init__()
#연산 정의
self.input_size = input_size
self.hidden_size = hidden_size
self.linear_1 = torch.nn.Linear(self.input_size, self.hidden_size)
self.relu = torch.nn.ReLU()
self.linear_2 = torch.nn.Linear(self.hidden_size, 1)
self.sigmoid = torch.nn.Sigmoid()
#정의 된 연산 동작 실행
def forward(self, input_tensor):
linear1 = self.linear_1(input_tensor)
relu = self.relu(linear1)
linear2 = self.linear_2(relu)
output = self.sigmoid(linear2)
return output
model = NeuralNet(2,5)
learning_rate = 0.03
criterion = torch.nn.BCELoss() #오차함수
epochs = 2000
optimizer = torch.optim.SGD(model.parameters(), lr = learning_rate)
model.eval()
test_loss_before = criterion(model(x_test).squeeze(), y_test)
print('before training, test loss is {}'.format(test_loss_before.item()))
before training, test loss is 0.74961918592453
for epoch in range(epochs):
model.train() #학습모드 변경
optimizer.zero_grad() #경삿값 0으로 설정
train_output = model(x_train) #학습데이터를입력하고 결괏값 계산
train_loss = criterion(train_output.squeeze(), y_train) #결과값의 차원을 레이블의 차원과 같게 만들고 오차 계산
if epoch % 100 == 0:
print('train loss at {} is {}'.format(epoch, train_loss.item()))
#오차함수를 가중치로 미분하여 오차가 최소가 되는 방향을 구하고 그 방향으로 모델을 학습률만큼 이동
train_loss.backward()
optimizer.step()
#optimizer.step()은 함수를 부를때마다 가중치를 학습률 만큼 갱신한다. 그래서 torch.optim.SGD에
#model.parameters() 함수로 추출한 모델 내부의 가중치와 학습률을 입력한다
train loss at 0 is 0.7472511529922485
train loss at 100 is 0.6543059945106506
train loss at 200 is 0.5940688848495483
train loss at 300 is 0.5288674831390381
train loss at 400 is 0.4591083526611328
train loss at 500 is 0.38283759355545044
train loss at 600 is 0.3155513107776642
train loss at 700 is 0.26354870200157166
train loss at 800 is 0.22371014952659607
train loss at 900 is 0.19243332743644714
train loss at 1000 is 0.1676136553287506
train loss at 1100 is 0.1474803388118744
train loss at 1200 is 0.13101942837238312
train loss at 1300 is 0.11747006326913834
train loss at 1400 is 0.10626258701086044
train loss at 1500 is 0.0969252660870552
train loss at 1600 is 0.08900205045938492
train loss at 1700 is 0.08219076693058014
train loss at 1800 is 0.07627519220113754
train loss at 1900 is 0.07109779864549637
model.eval()
test_loss = criterion(torch.squeeze(model(x_test)), y_test)
print('after train test loss is {}'.format(test_loss.item()))
after train test loss is 0.04989417642354965
torch.save(model.state_dict(), './model.pt')
print('state_dict {}'.format(model.state_dict()))
state_dict OrderedDict([('linear_1.weight', tensor([[-1.3987, -1.5754],
[-1.9068, 1.2278],
[-0.5247, -0.1774],
[ 1.1834, -1.9451],
[ 0.3384, 0.0094]])), ('linear_1.bias', tensor([-0.1826, -0.1612, 0.6616, -0.1489, -0.5376])), ('linear_2.weight', tensor([[-2.0049, 2.1084, 0.5376, 2.1987, 0.0672]])), ('linear_2.bias', tensor([-1.8519]))])
new_model = NeuralNet(2,5)
new_model.load_state_dict(torch.load('./model.pt'))
new_model.eval()
print